Generative models

_{^{4 min read (653 words)}}

Supervised models have achieved incredible results in various image tasks. They are straightforward and the correct outputs are accurately associated after their training [1]. In contrast, unsupervised learning sets the goal to investigate datasets without including samples without labels. This branch is arguably more similar to human learning, where relatively scarce information is provided to determine the parameters of complex models [2]. Although less accepted in practice nowadays, it is probably more meaningful for deep learning in the long perspective. It opens an opportunity of utilizing a potentially endless number of unlabeled images (or other signals). By learning the hierarchy of representations, downstream these features for distinct supervised tasks are realizable.

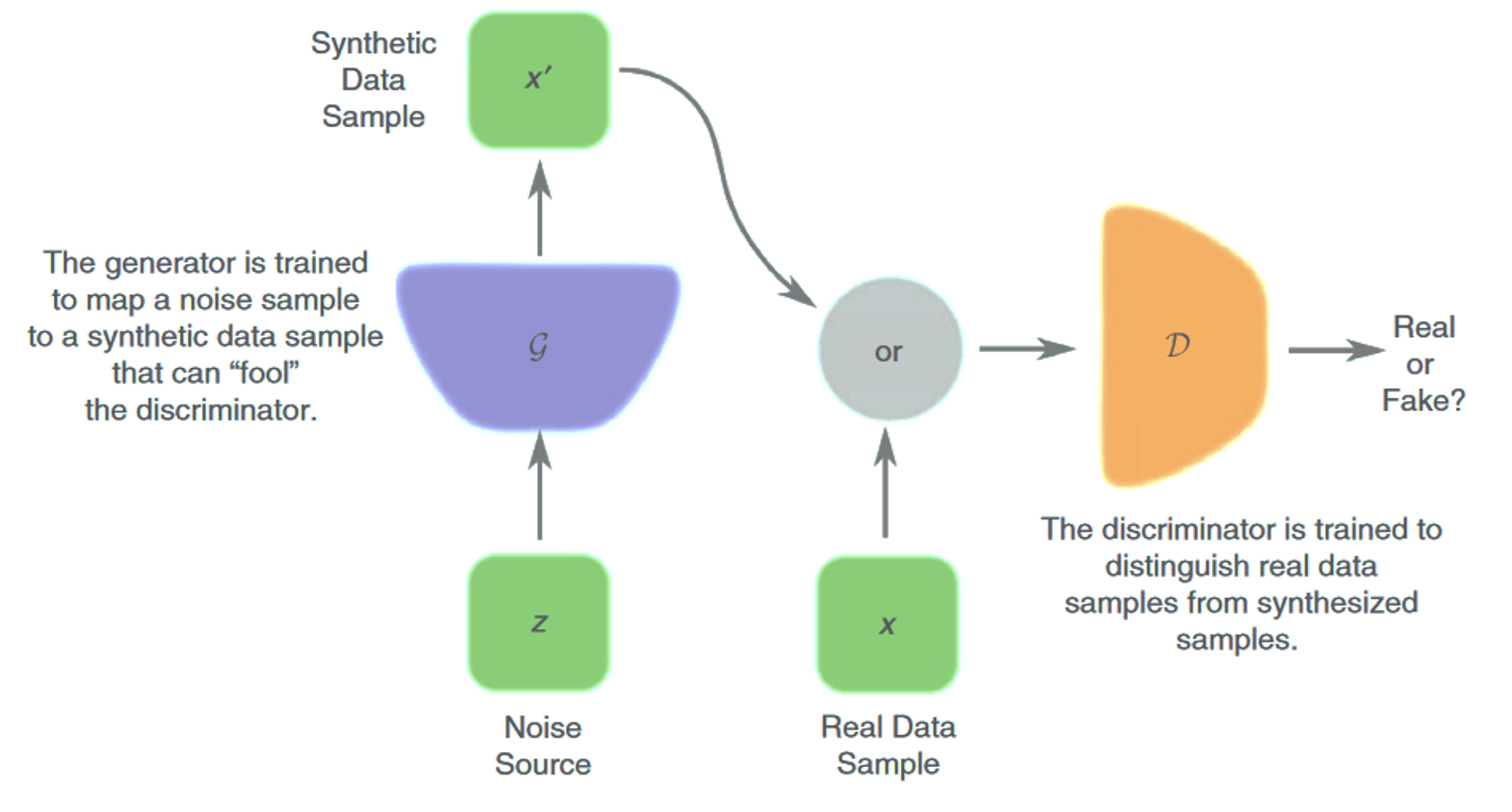
One known approach to unsupervised learning could be the clustering of unlabeled data into categories [3]. Another approach is modeling with generator networks, which transforms \(z\) latent variables to x samples. Here, \(g(z; θ^{(g)})\) differential function is normally described by the network. Variational autoencoders [4, 5], introduced for unsupervised learning, is a learning algorithm with stochastic variational inference. It can be optimized with gradient-based methods and was demonstrated to work with intractable cases. Despite the framework’s simplicity and theoretical evidence, it results in blurry images after the network optimization. Among the possible causes of this phenomenon could be the nature of relative entropy minimization of the distribution [6]. Later, the generative adversarial network [1] became one of the most successful generative models in research settings. Based on the game theory approach, optimization holds the competition between two networks. The generator creates \(x = g(z; θ^{(g)})\) samples, and the discriminator network produces \(d(x;θ^{(d)})\), a probability of \(x\)representing a real training example, in lieu of a fake set. The convergence of generator network:

given a function \(v(θ^{(g)}, θ^{(d)})\) describing the discriminator reward and generator ensuring \(-v(θ^{(g)},θ^{(d)})\) as its own. The standard option for \(v\):

This formulation encourages the generator to produce samples close to real, and the discriminator to masterly distinguish between real and fake examples. Ideally, after the generator is trained enough to create samples with no difference from the real, the discriminator part can be neglected.

GANs have been challenging to train in practice. Non-convergence was reported as an issue, where it is not certain for the cost of both networks to arrive at an equilibrium state [1], resulting in unstable training. Since then, several efforts have been suggested to improve stability: careful design [3], integration of additional techniques [7], conditioning with prior information [8], and introducing distributions measurement for easier convergence [9].

Super-resolution is one of the early and successful applications of GANs. Compared to previous optimization methods, SRGAN [10] could achieve high-frequency details and perceptually pleasant quality. This framework utilizes convolutional neural network architectures in both generator and discriminator branches to map very high complexities [11, 12]. As its lost function of generator network, a combination of content and adversarial losses was incorporated.

Super-resolution is a subclass of inverse problems in imaging. Usually, a high-resolution source can be subject to a degradation process, and more often the parameter defining it is unknown:

given \(I_y\) is the corresponding high-resolution image pair of low-resolution \(I_x\) and \(\delta\) is the unknown parameter function of the degradation process \(D\). Hence, the function \(\mathcal{F}\) of super-resolution can be modeled with parameters \(\theta\):

given \(\mathcal{F}\) is the super-resolution model and \(\theta\) denotes the parameters of \(\mathcal{F}\). Inverse operator \(\hat{\theta}\) can be predicted by solving:

given \(I_y\) actual and \(\hat{I_y}\) predicted high-resolution images for user defined cost \(L\), and \(\lambda \Phi(\theta)\) shows the regularization function.

Generative adversarial networks have been widely applied to other representatives of inverse imaging categories, including image denoising [13, 14], image inpainting [15, 16], and image reconstruction [17, 18]. Although GANs have a limitation, such as performance evaluation [6, 19], they have been proven an excellent tool in directions, where many correct answers are possible for the same input. A few of these could involve image translation [20], generating video sequences [21], and filling gaps in image [22] applications.

Fig. 1. Principle of generative adversarial network

How to cite

Askaruly, S. (2021). Generative models. Tuttelikz blog: tuttelikz.github.io/blog/2022/01/generative

References

[1] Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A. and Bengio, Y., 2020. Generative adversarial networks. Communications of the ACM, 63(11), pp.139-144.
[2] Murphy, K.P., 2012. Machine learning: a probabilistic perspective. MIT press.
[3] Radford, A., Metz, L. and Chintala, S., 2015. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.
[4] Rezende, D.J., Mohamed, S. and Wierstra, D., 2014, June. Stochastic backpropagation and approximate inference in deep generative models. In International conference on machine learning (pp. 1278-1286). PMLR.
[5] Kingma, D.P. and Welling, M., 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
[6] Theis, L., Oord, A.V.D. and Bethge, M., 2015. A note on the evaluation of generative models. arXiv preprint arXiv:1511.01844.
[7] Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A. and Chen, X., 2016. Improved techniques for training gans. Advances in neural information processing systems, 29.
[8] Mirza, M. and Osindero, S., 2014. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784.
[9] Arjovsky, M., Chintala, S. and Bottou, L., 2017, July. Wasserstein generative adversarial networks. In International conference on machine learning (pp. 214-223). PMLR.
[10] Ledig, C., Theis, L., Huszár, F., Caballero, J., Cunningham, A., Acosta, A., Aitken, A., Tejani, A., Totz, J., Wang, Z. and Shi, W., 2017. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4681-4690).
[11] Simonyan, K. and Zisserman, A., 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
[12] Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V. and Rabinovich, A., 2015. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1-9).
[13] Yang, Q., Yan, P., Zhang, Y., Yu, H., Shi, Y., Mou, X., Kalra, M.K., Zhang, Y., Sun, L. and Wang, G., 2018. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE transactions on medical imaging, 37(6), pp.1348-1357.
[14] Wolterink, J.M., Leiner, T., Viergever, M.A. and Išgum, I., 2017. Generative adversarial networks for noise reduction in low-dose CT. IEEE transactions on medical imaging, 36(12), pp.2536-2545.
[15] Yu, J., Lin, Z., Yang, J., Shen, X., Lu, X. and Huang, T.S., 2018. Generative image inpainting with contextual attention. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 5505-5514).
[16] Demir, U. and Unal, G., 2018. Patch-based image inpainting with generative adversarial networks. arXiv preprint arXiv:1803.07422.
[17] Chen, Y., Shi, F., Christodoulou, A.G., Xie, Y., Zhou, Z. and Li, D., 2018, September. Efficient and accurate MRI super-resolution using a generative adversarial network and 3D multi-level densely connected network. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 91-99). Springer, Cham.
[18] Dar, S.U.H., Yurt, M., Shahdloo, M., Ildız, M.E. and Çukur, T., 2018. Synergistic reconstruction and synthesis via generative adversarial networks for accelerated multi-contrast MRI. arXiv preprint arXiv:1805.10704.
[19] Wu, Y., Burda, Y., Salakhutdinov, R. and Grosse, R., 2016. On the quantitative analysis of decoder-based generative models. arXiv preprint arXiv:1611.04273.
[20] Zhu, J.Y., Park, T., Isola, P. and Efros, A.A., 2017. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE international conference on computer vision (pp. 2223-2232).
[21] Mathieu, M., Couprie, C. and LeCun, Y., 2015. Deep multi-scale video prediction beyond mean square error. arXiv preprint arXiv:1511.05440.
[22] Yeh, R., Chen, C., Lim, T.Y., Hasegawa-Johnson, M. and Do, M.N., 2016. Semantic image inpainting with perceptual and contextual losses. arXiv preprint arXiv:1607.07539, 2(3).